
天燕纳米材料密度泛函计算软件
软件介绍:
SHINE-DFT是基于密度泛函理论的量子力学程序,在投影缀加波的方法上,采用均匀实空间网格表示电子波函数,显著的提高体系的伸缩性和计算的收敛性。有效原子轨道使用了更加精确的网格,大大提高计算的精度和灵活性。通过程序中的密度泛函理论(DFT)可以研究材料的基态性质,含时密度泛函理论(TDDFT)研究材料的激发态性质。
计算对象:
能够计算金属、半导体、氧化物或者多种结构混合的超晶格及其含有缺陷的原子等体系。
计算功能:
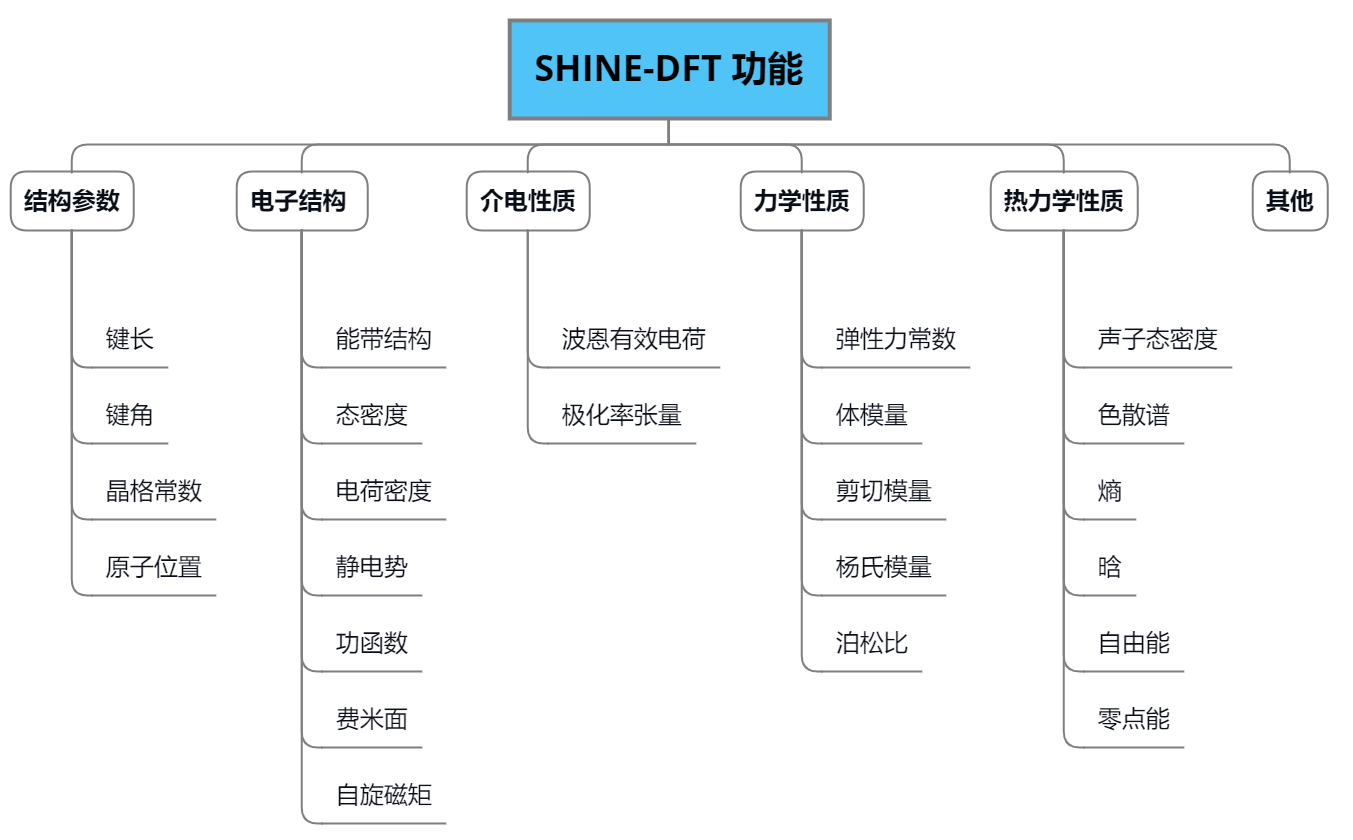
计算流程:
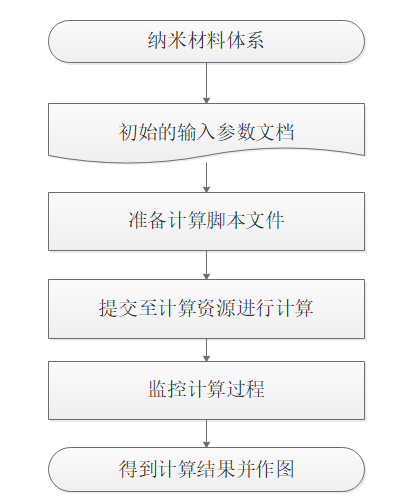
输入输出:
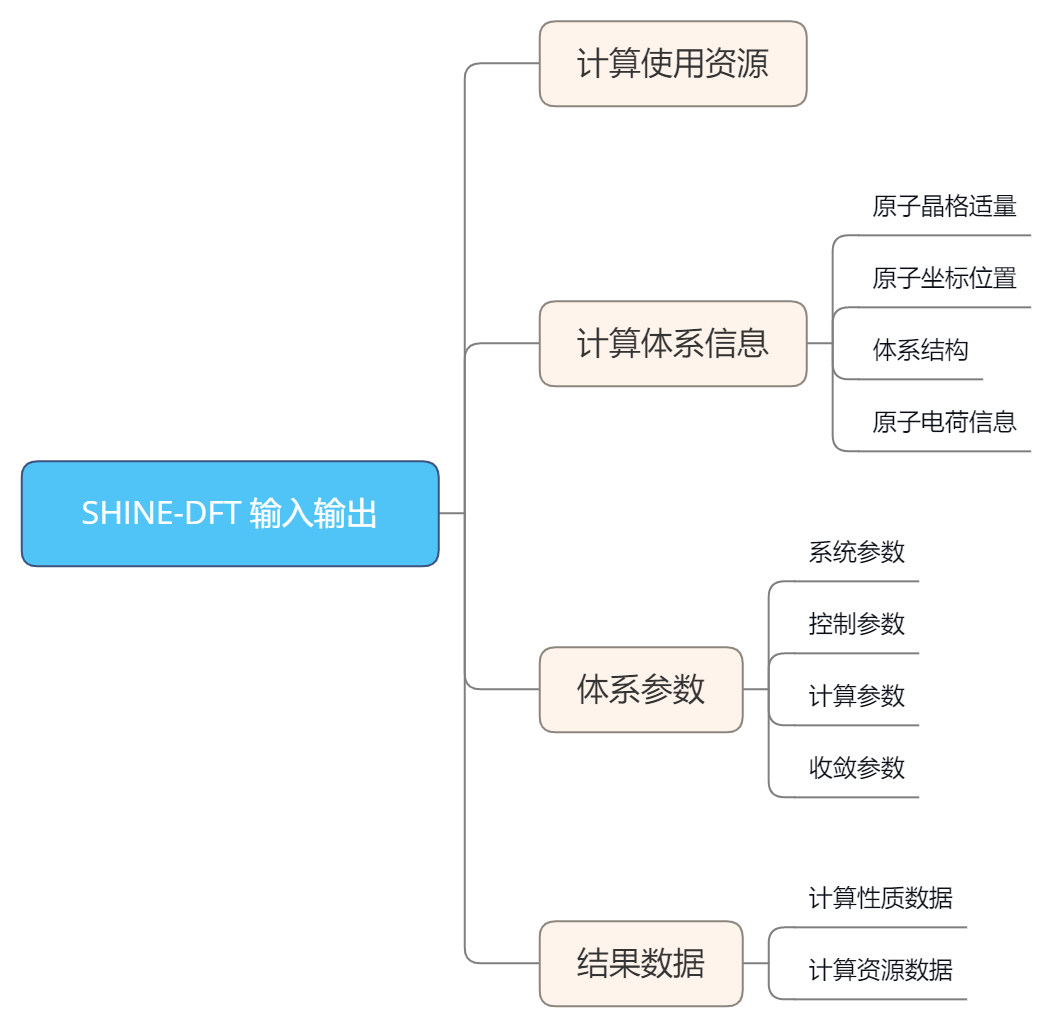
应用案例:
材料结构优化:
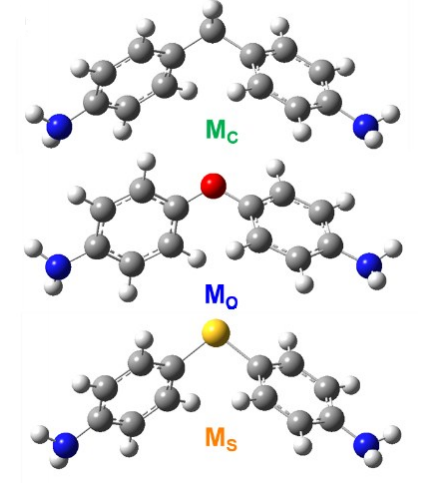 描述:通过DFT方法优化孤立的分子结构
描述:通过DFT方法优化孤立的分子结构
分子轨道空间分布:
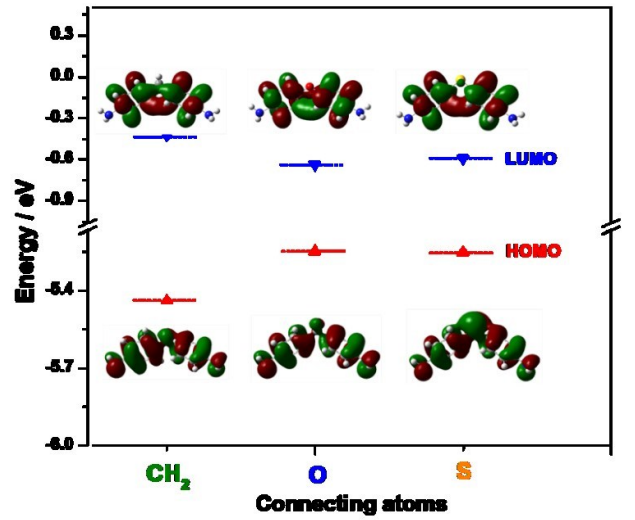 描述:分子轨道的HOMO-LUMO能级空间分布
描述:分子轨道的HOMO-LUMO能级空间分布
吸收光谱性质:
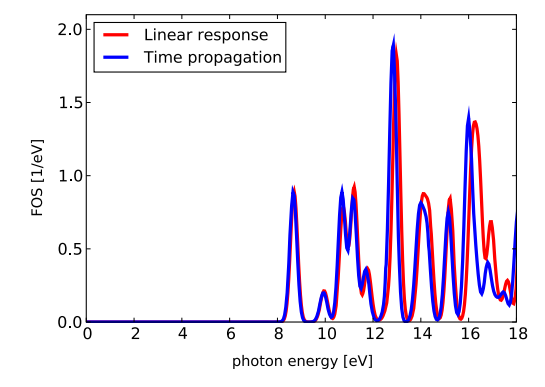 描述:通过时间传播和线性响应方法计算CH4分子的吸收光谱
描述:通过时间传播和线性响应方法计算CH4分子的吸收光谱
光电子界面:
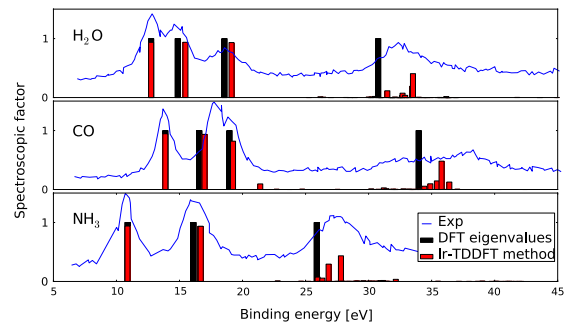 描述:光电子界面的计算对比:实验 & DFT方法 & TDDFT方法
描述:光电子界面的计算对比:实验 & DFT方法 & TDDFT方法
输运性质:
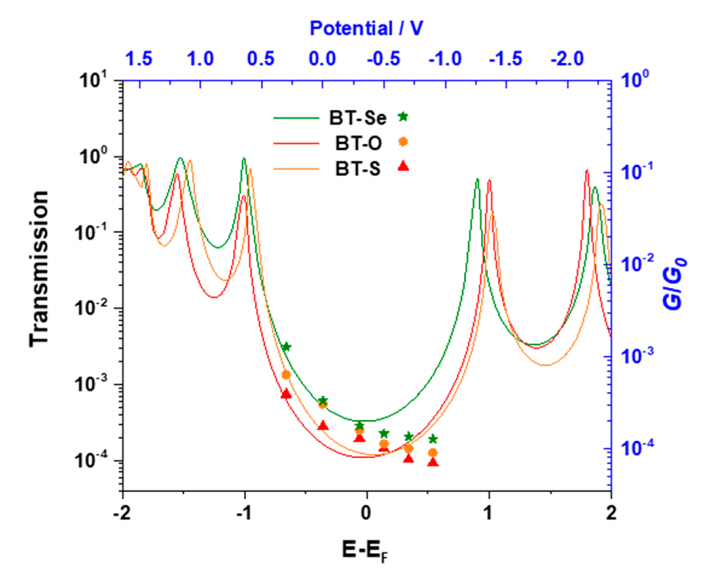 描述:门压控制下的电导和电子透射谱性质
描述:门压控制下的电导和电子透射谱性质
参考文献:
[1] Chen J, Thygesen K S, Jacobsen K W. Ab initio nonequilibrium quantum transport and forces with the
real-space
projector augmented wave method[J]. Physical Review B, 2012, 85(15): 155140.
[2] Kohn W and Sham L J 1965 Self-consistent equations including exchange and correlation effects Phys.
Rev. 140 A1133–8
[3] Runge E and Gross E K U 1984 Density-functional theory for time-dependent systems Phys. Rev. Lett.
52 997–1000
[4] Phillips J C and Kleinman L 1959 New method for calculating wavefunctions in crystals and molecules
Phys. Rev. 116
287–94
[5] Kleinman L and Bylander D M 1982 Efficacious form for model pseudopotentials Phys. Rev. Lett. 48
1425–8
[6] Vanderbilt D 1990 Soft self-consistent pseudopotentials in a generalized eigenvalue formalism Phys.
Rev. B 41 7892–5
[7] Bl¨ochl P E 1994 Projector augmented-wave method Phys. Rev. B 50 17953–79
[8] Wimmer E, Krakauer H, Weinert M and Freeman A J 1981 Full-potential self-consistent
linearized-augmented-plane-wave
method for calculating the electronic structure of molecules and surfaces: O2 molecule Phys. Rev. B 24
864–75
[9] Payne M C, Teter M P, Allan D C, Arias T A and Joannopoulos J D 1992 Iterative minimization
techniques for ab initio
total-energy calculations: molecular dynamics and conjugate gradients Rev. Mod. Phys. 64 1045–96
[10] Hehre W J, Stewart R F and Pople J A 1969 Self-consistent molecular-orbital methods. i. Use of
Gaussian expansions
of Slater-type atomic orbitals J. Chem. Phys. 51 2657–64
[11] Soler J M, Artacho E, Gale J D, Garc´ıa A, Junquera J, Ordej´on P and S´anchez-Portal D 2002 The
SIESTA method for
ab initio order-N materials simulation J. Phys.: Condens. Matter 14 2745
[12] Blum V, Gehrke R, Hanke F, Havu P, Havu V, Ren X, Reuter K and Scheffler M 2009 Ab initio molecular
simulations
with numeric atom-centered orbitals Comput. Phys. Commun. 180 2175–96
[13] Chelikowsky J R, Troullier N and Saad Y 1994 Finite-difference-pseudopotential method: electronic
structure
calculations without a basis Phys. Rev. Lett. 72 1240–3
[14] Beck T L 2000 Rev. Mod. Phys. 72 1041
[15] Junquera J, Paz O, S´ ´ anchez-Portal D and Artacho E 2001 Numerical atomic orbitals for
linear-scaling
calculations Phys. Rev. B 64 235111
[16] Briggs E L, Sullivan D J and Bernholc J 1996 Real-space multigrid based approach to large scale
electronic
structure calculations Phys. Rev. B 54 14362–75
[17] Enkovaara J E, Rostgaard C, Mortensen J J, et al. Electronic structure calculations with GPAW: a
real-space
implementation of the projector augmented-wave method[J]. Journal of Physics: Condensed Matter, 2010,
22(25): 253202.
[18] Wang Y H, Huang H, Yu Z, et al. Modulating electron transport through single-molecule junctions by
heteroatom
substitution[J]. Journal of Materials Chemistry C, 2020, 8(20): 6826-6831.
[19] Huang J R, Huang H, Tao C P, et al. Controlling Contact Configuration of Carboxylic Acid-Based
Molecular Junctions
Through Side Group[J]. Nanoscale research letters, 2019, 14(1): 1-7.
[20] Wang Y H, Yan F, Li D F, et al. Enhanced Gating Performance of Single-Molecule Conductance by
Heterocyclic
Molecules[J]. The journal of physical chemistry letters, 12: 758-763.
[21] Huang B, Liu X, Yuan Y, et al. Controlling and observing sharp-valleyed quantum interference effect
in single
molecular junctions[J]. Journal of the American Chemical Society, 2018, 140(50): 17685-17690.
[22] Peng L L, Chen F, Hong Z W, et al. Precise tuning of single molecule conductance in an
electrochemical
environment[J]. Nanoscale, 2018, 10(15): 7026-7032.